Elementary AI: Tic Tac Toe with Adversarial Search

In a previous post in my Elementary AI series, I discussed an implementation of language modeling with Markov Chains. Continuing my efforts to stay sharp with AI concepts, I wanted to delve a bit deeper into another important element of AI: Adversarial Search.

The most basic foundations of AI begin with the concept of search, like Uninformed Search (e.g. Breadth-first search, Depth-first search), Informed Search (e.g. A* search), and Local Search (e.g. Hill-climbing search). The main idea is that these families of algorithms explore “state spaces” i.e. possibilities in a variety of ways, and they evaluate those changes in order to achieve a certain goal. The most salient example is that of Google Maps; among many optimizations, it uses the A* search algorithm to find the best route between two points. Eventually, I would like to write another post exploring one or two of these algorithms.

In this post, I will focus on a different class of problems where the search algorithm has to take into account the actions of another agent, or “adversary.” These multi-agent environments where agents impact each other are often considered games. In AI, the most common types of games are those that are deterministic, turn-based, two-player games. There are various algorithms that have been developed for games and they are broadly categorized as adversarial search. The basic idea is that with games, you have to consider contigencies when determining what “moves” to make, based on what your opponent does. The simplest algorithm in this family is the Minimax algorithm, and I will use tic tac toe to demonstrate and walk through this method. I realize that tic tac toe is effectively an “un-winnable” game, unless one player makes a grave mistake or is very naive. That being said, this is just for practice and demonstration of Minimax, so it will work fine for that purpose.

Before stepping through Minimax in detail, let me introduce my tic tac toe abstraction first. The entire functionality of the game is built into a TicTacToe class. I’ll discuss some details, but all of the code is there for you to see and play around with too, if you like. This tic tac toe game uses a 2D NumPy 3x3 matrix as the board. Players interact with the board by calling the make_move method and entering the index that they want to place their letter (X or O) into. The index is implemented such that the top-left spot is 1, the top-center is 2, the top-left is 3, the center-left is 4, and so on. After players make a move, the player should call the ai_make_move method to let the AI move next. You simply alternate turns until the game is over. The TicTacToe class includes functions that do all the work to figure out when the game is over, who wins, etc.

The engine of the AI is the Minimax algorithm, as I mentioned. It’s one of the, if not the simplest form of adversarial search. The main idea is that the algorithm searches the game tree with the assumption that the opponent plays in an optimal manner. The Minimax algorithm that I implement here in this example is recursive. It performs a depth-first search of game tree, and when it reaches a terminal state, the outcome of the game is passed all the way back up as the recursion “unwinds.” Let me show you an example of a game tree and how Minimax works.

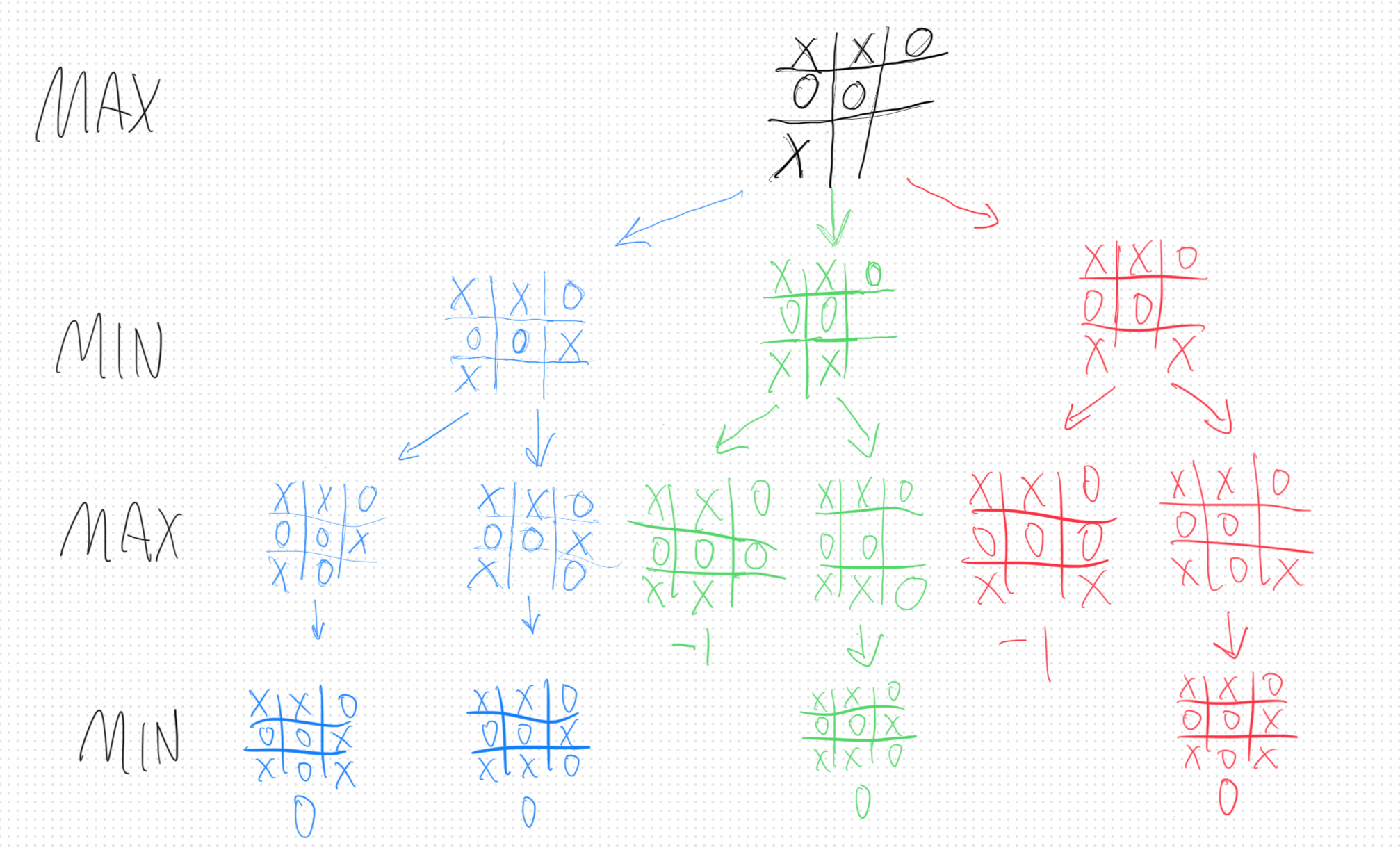
Starting at the very top, you have the current game state in the black writing, and it’s “Max’s” turn which you can see from the label. The way the algorithm works is that it explores the game tree depth-first - I’ve colored the paths in a way to make this easier to visualize. It will explore a path all the way down the tree, and at each turn Min or Max, the assumption is that the player will choose the move that is optimal for them, assuming their opponent also does the same. In this case, we define optimal as the move that results in the best outcome and that is determined by the terminal state of the game. I’ve drawn this example from the point of view of Max, who is X in this case. Games that end in a win for Max will be treated as having a value of 1, a draw results in a 0, and losses result in -1; these values are called utility values. So, Max has three possible moves in this game tree, and each path has a different color.

Starting with the blue, you can see that Min will have two options on his turn, both of which lead inevitably to draws. So at the bottom, Min will return the zeros back up to Max, who then passes that back to Min, and finally back up to Max at the top. So you can think of the blue choice having a utility value of 0 for Max. The green path is more interesting; one path leads to a victory for Min and one in a draw. So Min will chose the move with the lowest value which is -1 in this case. This results in the green path having a utility value of -1. The red path plays out similarly. So, you end up with the algorithm having searched the game tree and Max has to finally decide which move to make: blue of 0, green of -1, and red of -1. Max will take the path with the maximum value, so the move Max will make is the blue move.

And that is pretty much all there is to it. I will play a few games, one being naive and one playing for real so that you can see how it performs in practice. Thank you for taking the time to read and let me know what you think!

import numpy as np

class TicTacToeGame(object):
    def __init__(self, player) -> None:
        self.board = np.full((3,3), ' ')
        self.player = player
        self.ai = "x" if player == 'o' else 'o'

    def make_move(self, move) -> None:
        new_board = self.board.flatten()
        new_board[move-1] = self.player
        self.board = new_board.reshape((3,3))

    def ai_make_move(self, move) -> None:
        new_board = self.board.flatten()
        new_board[move-1] = self.ai
        self.board = new_board.reshape((3,3))

    def actions(self, board):
        return np.where(board.flatten() == ' ')[0] + 1

    def game_over(self, board):
        for seq in range(3):
            row_unique = np.unique(board[seq]).tolist()
            col_unique = np.unique(board[:, seq]).tolist()
            if len(row_unique) == 1 and row_unique != [' ']:
                return True, "Player" if self.player == row_unique[0] else "AI"
            if len(col_unique) == 1 and col_unique != [' ']:
                return True, "Player" if self.player == col_unique[0] else "AI"

        lr_diag_unique = np.unique(board.diagonal()).tolist()
        if len(lr_diag_unique) == 1 and lr_diag_unique != [' ']:
            return True, "Player" if self.player == lr_diag_unique[0] else "AI"

        rl_diag_unique = np.unique(np.flip(board, 1).diagonal()).tolist()
        if len(rl_diag_unique) == 1 and rl_diag_unique != [' ']:
            return True, "Player" if self.player == rl_diag_unique[0] else "AI"

        if " " not in np.unique(board).tolist():
            return True, "Draw"

        return False, None

    def utility(self, winner):
        result = {"AI": 1, "Player": -1, "Draw": 0}
        return result[winner]

    def result(self, board, action, player):
        new_board = board.flatten()
        new_board[action-1] = player
        new_board = new_board.reshape((3,3))
        return new_board

    def max_value(self, board):
        result, winner = self.game_over(board)
        if result:
            return self.utility(winner)
        v = -777
        for a in self.actions(board):
            v = max([v, self.min_value(self.result(board, a, self.ai))])
        return v

    def min_value(self, board):
        result, winner = self.game_over(board)
        if result:
            return self.utility(winner)
        v = 777
        for a in self.actions(board):
            v = min([v, self.max_value(self.result(board, a, self.player))])
        return v

    def minimax_decision(self, board):
        actions = self.actions(board)
        best_action_ix = np.argmax(np.array([self.min_value(self.result(board, a, self.ai)) for a in actions]))
        self.ai_make_move(actions[best_action_ix])

def player_move(move):
    game.make_move(move)
    print(game.board)

    result, winner = game.game_over(game.board)
    if result:
        print(f"Winner is: {winner}!") if winner != "Draw" else print("Game ends in a Draw!")

def ai_move():
    game.minimax_decision(game.board)
    print(game.board)

    result, winner = game.game_over(game.board)
    if result:
        print(f"Winner is: {winner}!") if winner != "Draw" else print("Game ends in a Draw!")

Playing Naively

game = TicTacToeGame('x')
print(f"Player is {game.player}")
print(f"AI is {game.ai}")

Player is x
AI is o

player_move(1)

[['x' ' ' ' ']
 [' ' ' ' ' ']
 [' ' ' ' ' ']]

ai_move()

[['x' ' ' ' ']
 [' ' 'o' ' ']
 [' ' ' ' ' ']]

player_move(2)

[['x' 'x' ' ']
 [' ' 'o' ' ']
 [' ' ' ' ' ']]

ai_move()

[['x' 'x' 'o']
 [' ' 'o' ' ']
 [' ' ' ' ' ']]

player_move(4)

[['x' 'x' 'o']
 ['x' 'o' ' ']
 [' ' ' ' ' ']]

ai_move()

[['x' 'x' 'o']
 ['x' 'o' ' ']
 ['o' ' ' ' ']]
Winner is: AI!

Playing wisely

game = TicTacToeGame('x')
print(f"Player is {game.player}")
print(f"AI is {game.ai}")

Player is x
AI is o

player_move(5)

[[' ' ' ' ' ']
 [' ' 'x' ' ']
 [' ' ' ' ' ']]

ai_move()

[['o' ' ' ' ']
 [' ' 'x' ' ']
 [' ' ' ' ' ']]

player_move(6)

[['o' ' ' ' ']
 [' ' 'x' 'x']
 [' ' ' ' ' ']]

ai_move()

[['o' ' ' ' ']
 ['o' 'x' 'x']
 [' ' ' ' ' ']]

player_move(7)

[['o' ' ' ' ']
 ['o' 'x' 'x']
 ['x' ' ' ' ']]

ai_move()

[['o' ' ' 'o']
 ['o' 'x' 'x']
 ['x' ' ' ' ']]

player_move(2)

[['o' 'x' 'o']
 ['o' 'x' 'x']
 ['x' ' ' ' ']]

ai_move()

[['o' 'x' 'o']
 ['o' 'x' 'x']
 ['x' 'o' ' ']]

player_move(9)

[['o' 'x' 'o']
 ['o' 'x' 'x']
 ['x' 'o' 'x']]
Game ends in a Draw!